基于大衍数构造的稀疏校验矩阵LDPC误码率matlab仿真,对比不同译码迭代次数,码率以及码长

1.引言

2.算法测试效果

3.算法涉及理论知识概要

4.MATLAB核心程序

5.完整算法代码文件获得

1.引言

基于大衍数的LDPC校验矩阵构造，本质是利用大衍数序列的周期性和互素性，设计具有规则稀疏结构的校验矩阵，兼顾性能与实现复杂度。基于大衍数列构造准循环低密度校验码的方法，该方法利用大衍数列固定项差对应的值单调递增的特点，构造出的校验矩阵具有准循环结构，节省了校验矩阵的存储空间。

2.算法测试效果

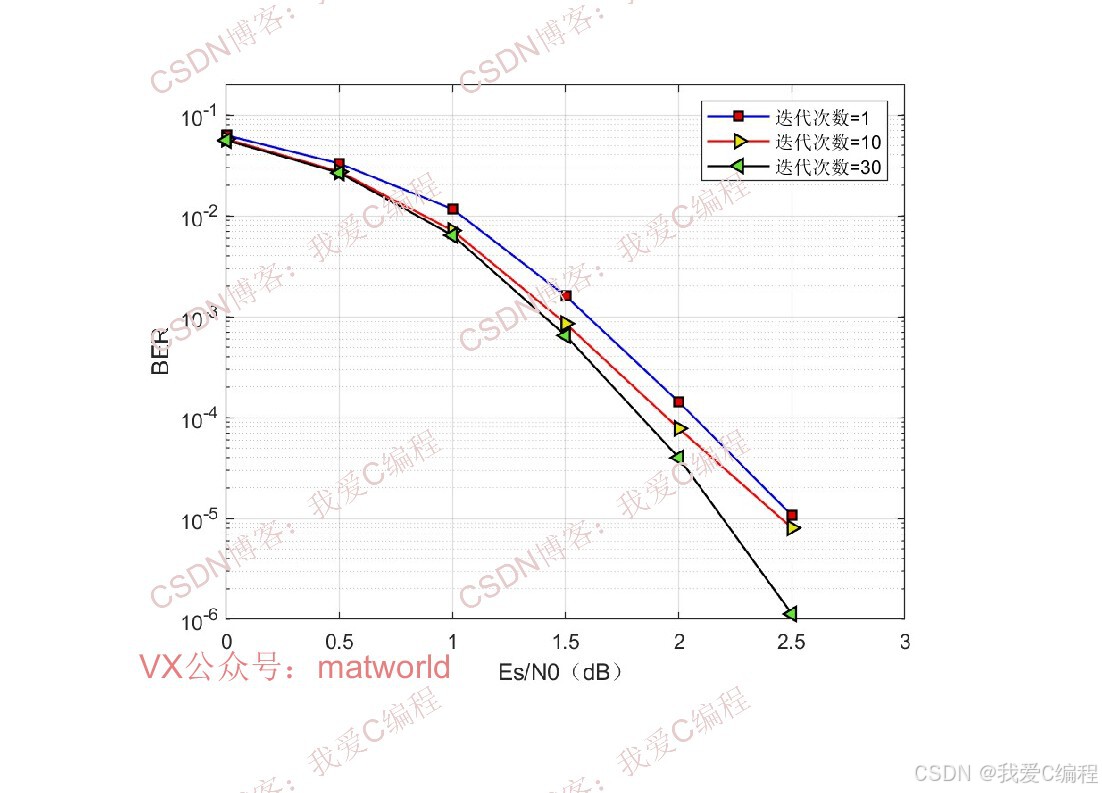
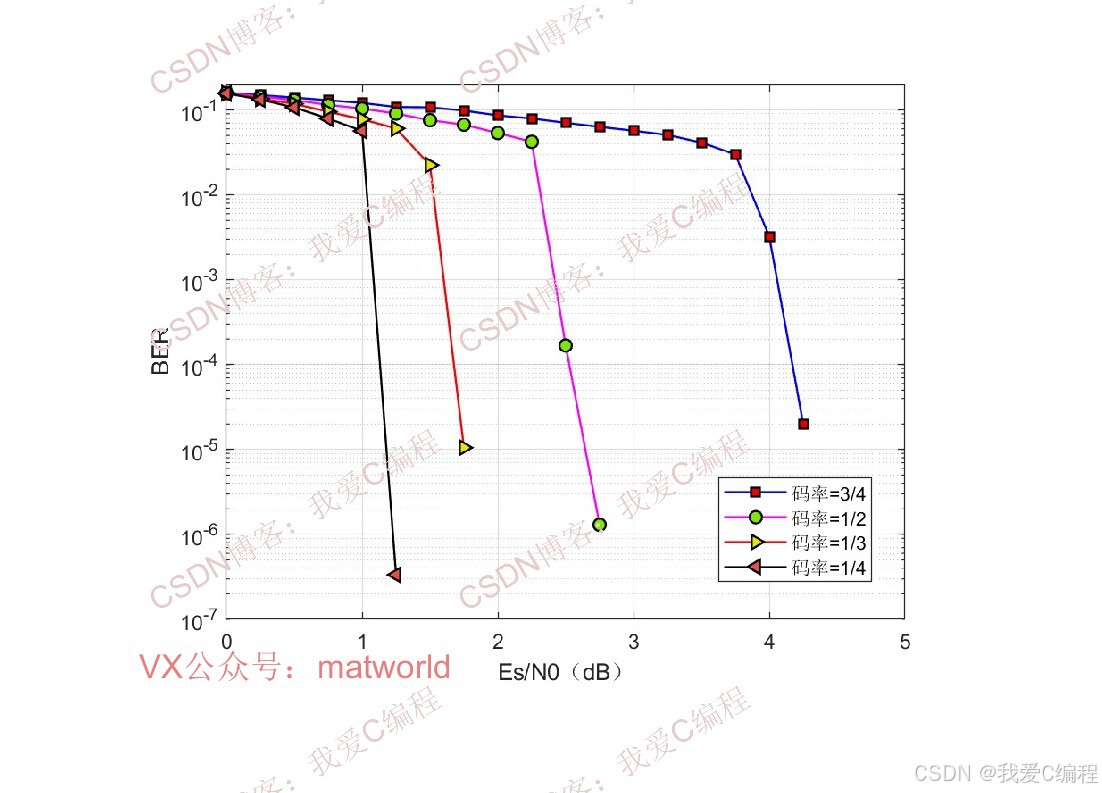
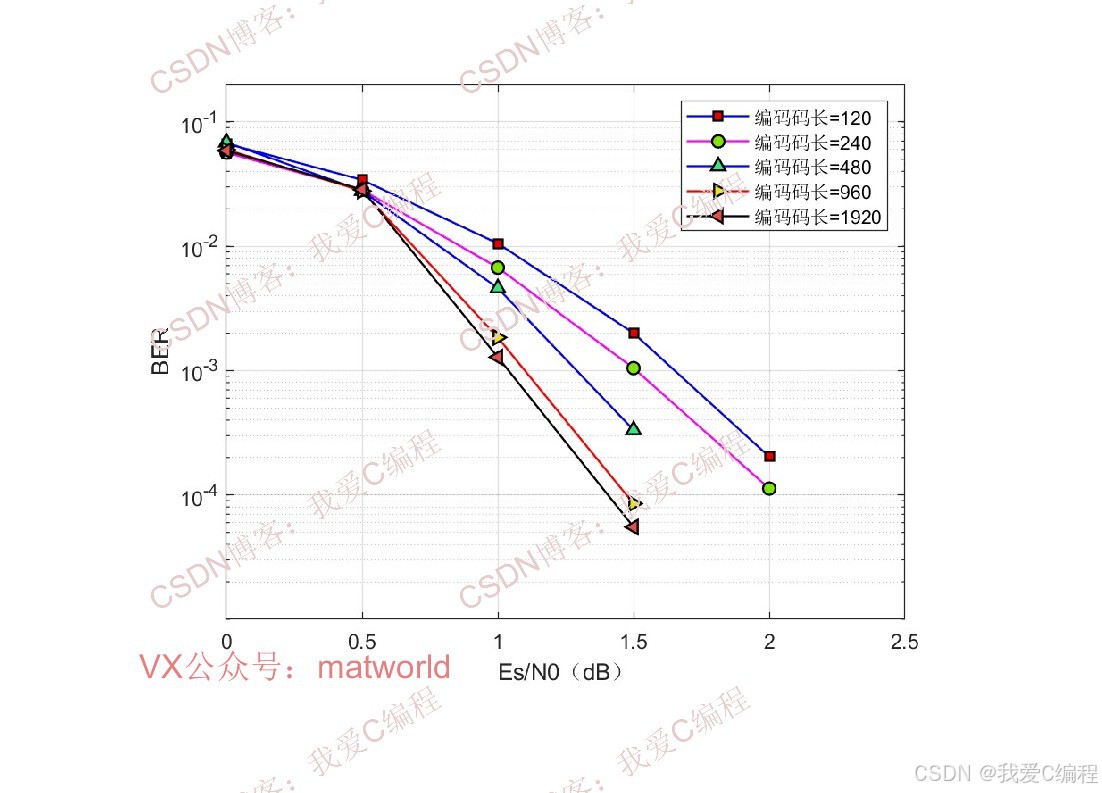
3.算法涉及理论知识概要

LDPC码是一类线性分组码，其编码和译码过程基于校验矩阵H和生成矩阵G实现。

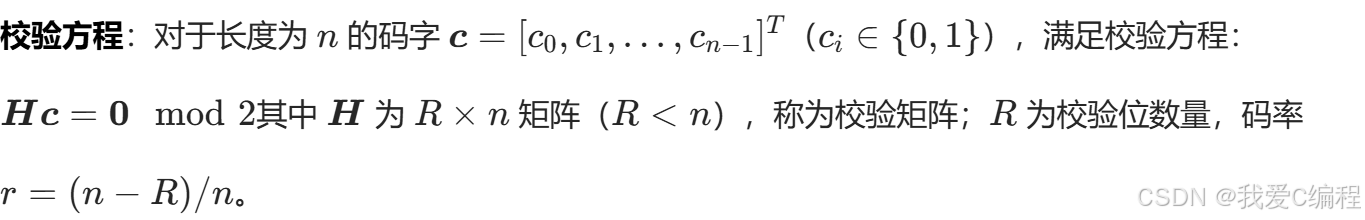
LDPC码的校验矩阵需满足行重dr 和列重dc均为小常数，即每行中1的个数为dr，每列中1的个数为 dc。行重和列重满足关系：R×dr=n×dc该公式体现了矩阵中1的总数的守恒性。

基于大衍数的LDPC校验矩阵构造，是将大衍数序列的元素映射为校验矩阵中1的位置，通过控制序列的周期性和互素性，确保矩阵满足稀疏性、行/列重恒定、行向量线性无关等核心要求。其核心思想可概括为：

**1.参数初始化：**码长n、码率r，计算校验行数R=n(1−r) ；设定行重dr和列重dc，满足Rdr=ndc 。

**2.大衍数序列生成：**选择基值K和周期M，生成扩展大衍数序列D(i,j)，其中i∈[0,R−1]对应矩阵行索引，j∈[0,n−1]对应矩阵列索引。

**3."1"的位置映射：**定义映射规则：若D(i,j)=t(t为预设阈值，通常取t=0)，则校验矩阵中H(i,j)=1 ；否则H(i,j)=0。

**4.矩阵验证与优化：**验证矩阵的行/列重是否恒定、行向量是否线性无关，若不满足则调整大衍数序列的参数(K,M,t)，直至满足要求。

利用大衍数列的独特性质设计指数矩阵，并将其用来扩展原模图矩阵，得到的校验矩阵中不存在四环。因为原模图基矩阵由计算机搜索算法产生，具有列数可灵活改变的优点，并且该方案构造的校验矩阵中六环的数量相比于基于大衍数列构造法大大地减少了。基于大衍数列构造准循环低密度校验码的方法.该方法利用大衍数列固定项差对应的值单调递增的特点,构造出的校验矩阵不含有长度为4的环,具有准循环结构,节省了校验矩阵的存储空间.

4.MATLAB核心程序

1............................................................
2    SNR     = 10^(EbN0(i)/10);
3    sigma   = 1/sqrt(SNR);
4    while Num_err <= NUMS(i)
5        fprintf('Eb/N0 = %f\n', EsN0(i));
6        Num_err
7        N0  = 2*10^(-EbN0(i)/10);
8        Trans_data             = round(rand(N-M,1));           %产生需要发送的随机数
9        [ldpc_code,newH]       = func_Enc(Trans_data,H1);       %LDPC编码
10        u                      = [ldpc_code;Trans_data];       %LDPC编码
11        Trans_BPSK             = 2*u-1;                        %BPSK
12 
13        NTrans_BPSK            = Trans_BPSK+sqrt(N0/2)*randn(size(Trans_BPSK));%加干扰
14        %译码
15        z_hat       = func_Ldpc_dec(NTrans_BPSK,sigma,newH,Max_iter);
16        x_hat       = z_hat(M+1:N);
17        %误码率
18        [nberr,rat] = biterr(x_hat,Trans_data);
19 
20        Num_err     = Num_err+nberr;
21        Numbers     = Numbers+1;
22
23figure;
24semilogy(EsN0,Bit_err,'o-');%显示波形
25xlabel('Es/N0（dB）');
26ylabel('BER');
27grid on;
28save dat1.mat EsN0 Bit_err%保存数据
2914-44m

5.完整算法代码文件获得

（V关注后回复码：X109）

《基于大衍数构造的稀疏校验矩阵LDPC误码率matlab仿真,对比不同译码迭代次数,码率以及码长》是转载文章，点击查看原文。